Long long time ago, ed actually in 1943, US Army was recruiting a lot of soldiers. Each of the recruits had to be subject of some medical examination, and in particular they were tested against syphilis. However, performing a single test was quite expensive. Then they came up with the following idea. Pick blood samples from a group of soldiers, mix them into a one big sample and perform the test on it. If the test is positive, there is at least one infected soldier in the group. But if it is negative, we know that all of the soldiers in the group are healthy and we just saved a lot of tests. It becomes then an interesting problem to devise a method which uses this observation to find the exact group of infected recruits among all the candidates with some nice bound on the number of tests. Without any additional assumptions there is not much you can do (exercise: do you see why?) but in this case we expect that the number of infected candidates is quite small. Then in fact you can save a lot and this story gave rise to the whole area called group testing.

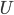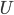Group testing is a rich field and includes a variety of models. Let us focus on the following one. We are given a universe and we want to find a hidden subset  of . We can aquire information only by asking queries to the intersection oracle, i.e., for a given subset , 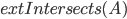answers true if and only if 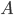has a nonempty intersection with . Moreover, we can decide which set we query based on previous answers. The goal is to use few queries. There are many algorithms for this problem, but I'm going to describe you my favourite one, called the bisecting algorithm. It dates back to early seventies and is due to Hwang, one of the fathers of combinatorial group testing. As you may expect from the name, it is a generalization of binary search. A simple observation is that once 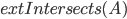answers false, we can safely discard 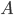and otherwise we know that 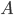contains at least one element of . So assume that in the algorithm we use a  oracle, implemented just as 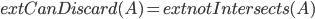. The algorithm works as in the animation below (choose FitPage in the zoom box and keep clicking the arrow down) :

So, basically, we have a partition of a universe (initially equal 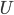) with the property that every set in the partition contains at least one element of . We examine sets of the partition one by one. Each set is divided into two halves and we query whether we can discard one of them. At some point we query a singleton and then we either discard it or find an element of . I hope it is clear now, but let me paste a pseudocode as well. How many queries do we perform? Let 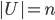and 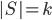. Call a query positive if the answer is Yes, negative otherwise. For a negative query  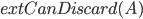we know that there is . Assign this query to . 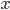Note that for every 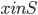there are  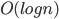queried sets assigned to it, because if we consider the queries in the order of asking them, every set is roughly  twice smaller than the previous one. So there are  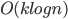negative queries. Every set 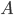from a positive query is a half of a set from a (different!) negative query, so the total number of positive queries is bounded by the total number of negative ones. Hence we have  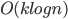 queries in total. A slightly more careful analysis (see Lemma 2.1 here) gives 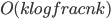. Cool, isn't it? Especially given that we hopefully do not expect a large fraction of infected soldiers...

Great, but is there a connection of all of that with the FPT algorithms from the title? Yes, there is one. Consider for example the k-PATH problem: given a graph and a number 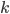we want to find a path of length 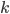. The corresponding decision problem is NP-complete, as a generalization of Hamiltonian Path. However, it turns out that when  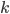is small, you can solve it pretty fast. Perhaps you know the famous Color Coding algorithm by Alon, Yuster and Zwick which solves it in 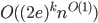. However, one can do better: Björklund, Husfeldt, Kaski and Koivisto presented a  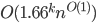-time Monte-Carlo algorithm! The only catch is that it only solves the decision problem. Indeed, it uses the Schwartz-Zippel lemma and when it answers YES, there is no way to trace back the path from the computation.

Now, let the universe 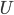  be the edge set of our graph. We want to find one of (possibly many) 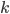-subsets of 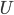corresponding to 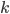-edge paths in our graph and the Björklund et al's algorithm is an inclusion oracle, which tells you whether a given set of edges contains one of these subsets. So this is not exactly the same problem as before, but sounds pretty similar... Indeed, again we can implement the   oracle, i.e., 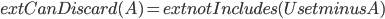. So it seems we can use the bisecting algorithm to find a 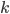-path with only  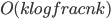queries to the decision algorithm! Correct?

Well, not exactly. The problem is the oracle is a Monte Carlo algorithm, more precisely it reports false negatives with probability at most, say, 1/4. Together with Andreas Björklund and Petteri Kaski we showed that a surprisingly simple patch to the bisecting algortihm works pretty nice in the randomized setting. The patch is as follows. Once the bisecting algorithm finishes in the randomized setting, we have a superset of a solution. Then, as long as we have more than 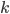 candidate elements, we pick one by one, in a FIFO manner, and check whether we can discard this single element. We show that the expected number of queries is 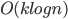. (Actually, we conjecture it is optimal, i.e., you have to loose a bit compared to the slightly better  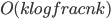 in the deterministic setting.) As a consequence, we get a pretty fast implementation of finding  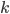-paths. For example, a (unique) 14-vertex path is found in a 1000-vertex graph well below one minute on a standard PC. Not bad for an NP-complete problem, I would say. Let me add that the Schwartz-Zippel approach is used in a number of FPT algorithms and in many cases the corresponding search problem can be cast in the inclusion oracle model mentioned above. Examples include k-packing, Steiner cycle, rural postman, graph motif and more.

If you want to learn more, see the paper or slides from my recent ESA talk!