Back in 2012, when I was a post-doc in Lugano, Switzerland, I was working with Fabrizio Grandoni and Monaldo Mastrolili on a pricing problem we called Hypermatching Assignment Problem. This problem is at the same time a generalization of the Generalized Assignment Problem and of the k-Set Packing problem, which brought my attention to the approximation status of the latter, being is the subject of this post.

k-Set Packing is a basic combinatorial optimization problem, where given a universe U and a family of its subsets F, we are to find a maximum subfamily of pairwise disjoint subsets of F. A special case of 3-Set Packing is the 3-Dimensional Matching problem. A good argument showing that those two problems are indeed classic is the fact that both belong to the Karp's list of 21 NP-hard problems.

A local search routine tries to locally modify a current solution in order to get a better one. For the k-Set Packing by p-local search, we denote an algorithm, which starts with an empty set A, and tries to improve it by adding a set A_0 of at most p new sets, such that the number of sets we need to remove in order to maintain a feasible solution is strictly smaller than the number of sets we have added. Having a local search maximum, our hope is to prove that an optimum solution is not much better.

It is easy to see, that a 1-local search maximum gives an inclusionwise maximum subfamily of F, which in turn implies an approximation ratio of k. It. is not hard to show, that a 2-local search maximum yields a (k+1)/2 approximation ratio. In 1989 Hurkens and Schrijver [SIDMA'89] have shown, that with growing values of p, a p-local search maximum gives (k+eps_p)/2 approximation, where eps_p is a constant depending on p converging to 0. Up to now this was the best known polynomial time approximation algorithm for both k-Set Packing and 3-Dimensional Matching.

Later in [SODA'95]  Halldorsson proved that when we consider logarithmic values of p, the approximation ratio is upper bounded by (k+2)/3, which was slightly improved in our Hypergraph Assignment Problem paper downto (k+1+eps)/3, showing that in quasipolynomial time one can break the 1.5-approximation ratio for 3-Dimensional Matching. A natural question is the following. Can we implement the O(log n)-local search in polynomial time? This brings us to the area of fixed parameter tractability, where we are aiming at a 2^O(r) poly(|F|) time algorithms. Unfortunately we have shown that the parameterized local search is W[1]-hard, even in the more relaxed permissive variant, which means that f(r)poly(|F|) time algorithm is unlikely to exist, no matter how fast growing the function f() is.

Therefore we have to modify our strategy. In our second take we try the following. First, we inspect the existing analyses of approximation ratios upper bounds to see what is the exact set of swaps, which our current solution needs to be impossible to improve with, in order for the proof to go through. Next, we want to show, that for this particular set of swaps we can implement the local search algorithm effectively.

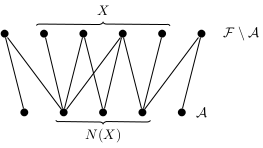
In the analysis of Halldorsson, a notion of a conflict graph is used. Imagine a bipartite graph with sets of our current solution A on one side, sets of FA on the other, where a set of A and a set of FA are connected by an edge if they share a common element.

Note that an edge indicates that it is impossible to have both sets at the same time in a solution. The main part of the analysis of Halldorsson is showing that if (k+2)/3|A| < |OPT|, then there exists a subset X of FA of size O(log n), such that |N(X)| < |X| in the conflict graph, that is the number of sets that we need to remove after adding sets of X is strictly smaller than the size of X itself. However, when inspected more closely the set X has some structure, that is G[N[X]] is a subdivision of one of the following graphs:

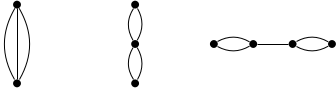This means that in our local search algorithm we do not have to look for all improving sets X of logarithmic size, but it is enough to consider sets X, such that G[N[X]] is of constant pathwidth! In this way by using the color coding technique of Alon, Yuster and Zwick [JACM'95] we obtain a polynomial time (k+2)/3 approximation algorithm. Unfortunatelly this is not yet enough to break the 1.5 approximation ratio for 3-Dimensional Matching, as the existing upper bound of (k+1+eps)/3 in fact uses improving sets of unbounded pathwidth. This is the main technical hurdle, overcoming which required proving lemmas relating pathwidth, average degree and girth of a graph. Finally, we have obtained a (k+1+eps)/3 polynomial time approximation algorithm for k-Set Packing, implying a 1.34-approximation for 3-Dimensional Matching.

The described results were obtained by Maxim Sviridenko & Justin Ward, published at ICALP'13, and by myself, to appear in FOCS'13 and available on arxiv. Since the papers contain significant intersection of ideas, we decided to prepare a common journal version. Personally I am very happy about the described result, because it utilizes techniques from the parameterized complexity in a nontrivial way, to obtain an improvement in a over 20 years old approximation ratio of a basic problem.