The dynamic Steiner tree problem has been around for a while already (for 24 years), but it did not get a satisfying answer from efficiency point of view, i.e., one would like to have a fast algorithm that maintains a constant approximate solution and allows to update the set of terminal vertices. On one hand, there have been some studies of the online version of this problem, where we focus on minimizing the number of changes to the tree that are necessary to maintain a good approximation. This line of research was started in the pioneering paper by Imase and Waxman [1] and was later continued in [2, 3, 4]. However, in the online problem one ignores the problem of efficiently finding these changes to the tree. On the other hand, the problem of maintaining a Steiner tree is also one of the important open problems in the network community [5], where it is often referred to as dynamic multi-cast tree problem. The motivating problem is to maintain a cheap communication network between a set of dynamically changing users. While it has been studied for many years, the research resulted only in several heuristic approaches [6, 7, 8, 9], none of which has been formally proved to be efficient.
In our paper "The Power of Dynamic Distance Oracles: Efficient Dynamic Algorithms for the Steiner Tree" we have shown the first sublinear time algorithm which maintains a constant approximate Steiner tree under terminal additions and deletions. We show that we can maintain a 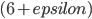 -approximate Steiner tree of a general graph in
-approximate Steiner tree of a general graph in 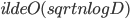 time per terminal addition or removal. Here,
time per terminal addition or removal. Here, 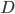 denotes the stretch of the metric induced by the graph. For planar graphs we achieve the same running time and the approximation ratio of
denotes the stretch of the metric induced by the graph. For planar graphs we achieve the same running time and the approximation ratio of 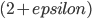 . Observe that due to the sparsity of real world networks only algorithms with such sublinear complexity could be of some practical importance and could potentially be used to reduce the communication cost of dynamic multicast trees. Our paper aims to be a theoretical proof of concept that from algorithmic complexity perspective such algorithms are indeed possible. However, turning these theoretical ideas into useful algorithms will require much more research. In particular, a natural question here is whether the approximation factor of our algorithms could be considerably improved while keeping the running time sublinear?
. Observe that due to the sparsity of real world networks only algorithms with such sublinear complexity could be of some practical importance and could potentially be used to reduce the communication cost of dynamic multicast trees. Our paper aims to be a theoretical proof of concept that from algorithmic complexity perspective such algorithms are indeed possible. However, turning these theoretical ideas into useful algorithms will require much more research. In particular, a natural question here is whether the approximation factor of our algorithms could be considerably improved while keeping the running time sublinear?
Let me note that this might be hard as the approximation factor of 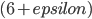 for Steiner tree in general graphs comes from using 3-approximate oracles [10], using 2-approximation of the Steiner tree by the MST in the metric closure, and
for Steiner tree in general graphs comes from using 3-approximate oracles [10], using 2-approximation of the Steiner tree by the MST in the metric closure, and 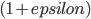 -approximate online MST algorithm. In other words we hit two challenging bounds: in order to improve our approximation factors, one would need either to improve the approximation ratio of the oracles which are believed to be optimal, or devise a framework not based on computing the MST. The second challenge would require to construct simple and fast (e.g., near-linear time) approximation algorithms for Steiner tree that would beat the MST approximation ratio of 2. Constructing such algorithms is yet another challenging open problem.
-approximate online MST algorithm. In other words we hit two challenging bounds: in order to improve our approximation factors, one would need either to improve the approximation ratio of the oracles which are believed to be optimal, or devise a framework not based on computing the MST. The second challenge would require to construct simple and fast (e.g., near-linear time) approximation algorithms for Steiner tree that would beat the MST approximation ratio of 2. Constructing such algorithms is yet another challenging open problem.
If you would like to learn more on how it works, you can still attend our talk during the coming STOC in Portland on Monday at 9:00, or have look into the full version of the paper on arXiv.
[1] M. Imase and B. M. Waxman. Dynamic Steiner tree problem. SIAM J. Discrete Math., 4(3):369–384, 1991.
[2] N. Megow, M. Skutella, J. Verschae, and A. Wiese. The power of recourse for online MST and TSP. In ICALP, pages 689–700. 2012.
[3] A. Gu, A. Gupta, and A. Kumar. The power of deferral: maintaining a constant-competitive Steiner tree online. In STOC, pages 525–534, 2013.
[4] A. Gupta and A. Kumar. Online Steiner tree with deletions. In SODA, pages 455–467. SIAM, 2014.
[5] X. Cheng, Y. Li, D.-Z. Du, and H. Ngo. Steiner trees in industry. In D.-Z. Du and P. Pardalos, editors, Handbook of Combinatorial Optimization, pages 193–216. Springer US, 2005.
[6] F. Bauer and A. Varma. ARIES: A rearrangeable inexpensive edge-based on-line Steiner algorithm. IEEE Journal of Selected Areas in Communications, 15:382–397, 1995.
[7] E. Aharoni and R. Cohen. Restricted dynamic steiner trees for scalable multicast in datagram networks. In INFOCOM ’97. Sixteenth Annual Joint Conference of the IEEE Computer and Communications Societies. Driving the Information Revolution., Proceedings IEEE, volume 2, pages 876–883 vol.2, Apr 1997.
[8] S.-P. Hong, H. Lee, and B. H. Park. An efficient multicast routing algorithm for delaysensitive applications with dynamic membership. In INFOCOM ’98. Seventeenth Annual Joint Conference of the IEEE Computer and Communications Societies. Proceedings. IEEE, volume 3, pages 1433–1440 vol.3, Mar 1998.
[9] S. Raghavan, G. Manimaran, C. Siva, and R. Murthy. A rearrangeable algorithm for the construction of delay-constrained dynamic multicast trees. IEEE/ACM Transactions on Networking, 7:514–529, 1999.
[10] M. Thorup and U. Zwick. Approximate distance oracles. J. ACM, 52(1):1–24, 2005.
