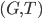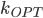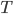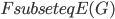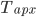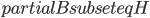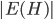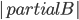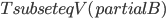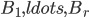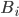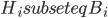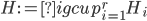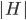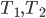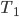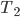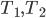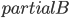Category Archives: focs 2014

Graph Isomorphism on graphs of bounded treewidth

Posted on by
Reply

The Graph Isomorphism problem is interesting for many reasons, one being the fact that its complexity status is still unclear - it is probably not NP-complete, but not known to be in P either. In the past decades, researchers identified a large number of special graph classes for which GI is polynomial-time solvable, including planar graphs, graphs of bounded maximum degree, and graphs excluding a fixed minor, among others.

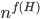A closer look at the known algorithms for graphs of bounded degree or graphs excluding a fixed minor reveals that the dependency in the running time bound on the "forbidden pattern" is quite bad: in the first case or in the second case, for some function 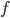. Seeing such dependencies, a natural question is: do there exist fixed-parameter algorithms, parameterized by the "forbidden pattern"? In other words, does the exponent in the polynomial factor in 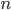need to depend on the pattern, on can we obtain an algorithm with running time ?

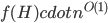This question remains widely open for all aforementioned cases of bounded degree or excluded minor. In our recent FOCS 2014 paper, we have answered the question affirmatively for the special case of bounded treewidth graphs, proving that isomorphism of two 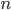-vertex graphs of treewidth 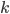can be tested in time .

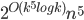As a starting point, observe that comparing (testing isomorphism) of two graphs together with their given tree decompositions (that is, we want to check if the whole structures consisting of a graph and its decomposition are isomorphic) can be done easily in time polynomial in the size of the graphs, and exponential in the width of the decompositions. This is a relatively standard, but tedious, exercise from the area of designing dynamic programming algorithms on tree decompositions: if you have seen a few of these, I guess you can figure out the details, but if you don't, this is probably one of the worst examples to start with, so just assume it can be done. Alternatively, you may use the recent results of Otachi and Schweitzer that say that one needs only a set of bags for the decomposition, even without the structure of the decomposition tree itself.

With this observation, the task of comparing two bounded-treewidth graphs reduces to the following: given a graph 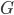of treewidth 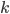, we would like to compute in an isomorphic-invariant way a tree decomposition of $G$ of near-optimal width. Here, isomorphic-invariant means that we do not want to make any decisions depending on the representation of the graph in the memory (like, "take arbitrary vertex"), and the output decomposition should be the same (isomorphic) for isomorphic input graphs. Given such an isomorphic-invariant treewidth approximation algorithm, we can now compute the decompositions of both input graphs, and compare given pairs (graph, its tree decomposition), as described in the previous paragraph. Note that for this approach we do not need to output exactly one tree decomposition; we can output, say, 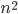of them, and compare every pair of decompositions for two input graphs for the Graph Isomorphism problem; we only need that the set of output decompositions is isomorphic invariant.

To cope with this new task, let us look at the known treewidth approximation algorithms; in particular, the arguably simplest one - the Robertson-Seymour algorithm. This algorithm provides a constant approximation in 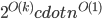time, where 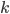is the treewidth of the input 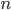-vertex graph 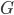. It is a recursive procedure that decomposes a part 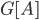of the input graph, given a requirement that a set 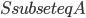should be contained in the top bag of the output decomposition. Think of as an interface to the rest of the graph; we will always have 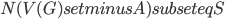, but for technical reasons the set could be larger. During the course of the algorithm we maintain an invariant .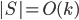

In the leaves of the recursion we have 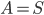, and we output a single bag 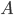. If is small, say, 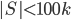, then we can add an arbitrary vertex to and recurse. The interesting things happen when grows beyond the threshold .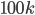

As the graph is of treewidth 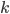, but 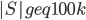, in an optimal decomposition of 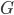the set is spread across many bags. A simple argument shows that there exists a bag 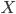, , 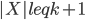such that every component of 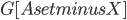contains at most 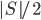vertices of . The algorithm takes 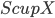as a root bag (note that 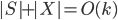), and recurses on every connected component of 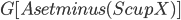; formally, for every connected component 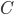of 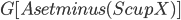, we recurse on 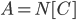with 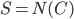. Since every component of 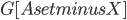contains at most 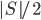vertices of , in every recursive call the new set is of size at most .

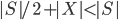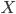In the above algorithm, there are two steps that are very deeply not isomorphic-invariant: "take an arbitrary vertex to " in the case of small , and "take any such " in the case of large . We start fixing the algorithm in the second, more interesting case.

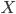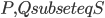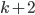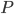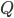Before we start, let us think how we can find such a set - the argument provided two paragraphs ago only asserted its existence. One of the ways to do it is to iterate through all disjoint sets of size exactly each, and check if the minimum separator between and in 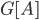is of size at most 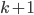(such a separator can contain vertices of 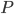or 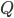, these are deletable as well). If such a separator is found, it is a good candidate for the set 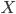- it does not necessarily have the property that every connected component of 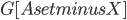contains at most half of the vertices of , but the claim that in the recursive calls the size of the set decreased is still true. 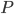Of course, in this approach we have two not isomorphic-invariant choices: the choice of and 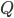, and the choice of the minimum separator .

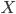Luckily, an (almost) isomorphic-invariant way to make the second choice has already been well understood: by submodularity of cuts, there exists a well-defined notion of the minimum cut closest to 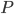, and the one closest to 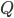. But how about the choice of 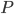and ?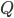

The surprising answer is: it works just fine if we just throw into the constructed bag all separators for every choice of 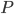and 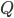. That is, we start with the tentative bag 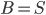, we iterate over all such (ordered) pairs 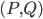, and throw into the constructed bag 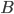the minimum cut between 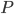and 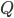that is closest to 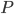, as long as it has size at most 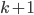. We recurse on all connected components of 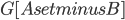as before; the surprising fact is that the sizes of the sets in the recursive calls did not grow. To prove this fact, we analyse what happens to the components of 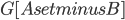when you add 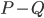cuts one-by-one; a single step of this induction turns out to be an elementary application of submodularity. Furthermore, note that if the size of is bounded in terms of 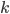, so is the set of the bag : .

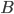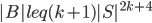Having made isomorphic-invariant the "more interesting" case of the Robertson-Seymour approximation algorithm, let us briefly discuss the case of the small set : we need to develop an isomorphic-invariant way to grow this set. Here, we need some preprocessing: by known tricks, we can assume that (a) the input graph does not contain any clique separators, and (b) if 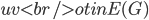, then the minimum cut between 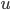and 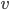is of size at most 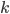. Furthermore, observe that in our algorithm, contrary to the original Robertson-Seymour algorithm, we always maintain the invariant that and 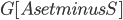is connected. 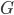Thus, is never a clique in , and, if 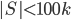, we can throw into a bag the minimum cut between 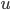and 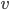that is closest to 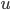, for every ordered pair 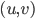where , .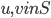

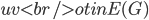In this way, the lack of clique separators ensures that we always make a progress in the algorithm, by "eating" at least one vertex of 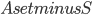. The bound on the size of minimum cut between two nonadjacent vertices ensures that the bag created in this way is of size 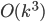, and so are the sets in the recursive calls. Consequently, our algorithm computes in an isomorphic-invariant way a tree decomposition with adhesions of size 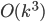and bags of size .

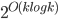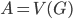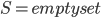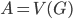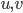Well, there is one small catch - neither of the aforementioned steps is good to start the algorithm, to provide the initial call of the recursion; the Robertson-Seymour approximation starts with just and . Here, we can start with and for every pair of nonadjacent vertices, as in this call the step with the small set will work fine. But this produces not a single isomorphic-invariant tree decomposition, but a family of 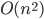decompositions - which is still fine for the isomorphism test.

A cautious reader would also notice that the described algorithm results in a double-exponential dependency on the parameter 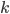in the running time, contrary to the claim of the 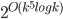term. Getting down to this dependency requires a bit more technical work; we refer to the full version of our paper for details.

How pineapples help finding Steiner trees?

Posted on by
Reply

The Bratislava Declaration of Young Researchers is something I was involved in recently. Its preparation was inspired by Slovak Presidency of the EU and it was presented on today's informal Council of Ministers responsible for competitiveness (Research). I hope this will have some follow up, as current trend in funding research in EU is in my opinion (and not only my as this declaration shows) going in the wrong direction.
Recently with Marcin Pilipczuk, Micha? Pilipczuk and Erik Jan van Leeuwen we were able to prove that the Steiner Tree problem has a polynomial kernel on unweighted planar graphs. So far this was one of few problems where such kernel seemed possible, but existing tools (e.g. theory of bidimensionality) were unable to deliver it. Essentially, we were able to prove the following theorem.

Theorem 1. Let be a planar Steiner tree instance, and let be the cost of optimum tree connecting terminals in the unweighted graph . One can in polynomial time find a set of edges of size polynomial in that contains an optimal Steiner tree connecting in .

cutopen Figure 1. The process of cutting open the graph along the tree .

Let us shortly discuss the idea of the proof of this theorem. The most non-trivial part of it is the pineapple decomposition. In order to give you a glimpse on this decomposition we will first reduce the problem to the simpler case where all terminals lie on one designated face. Such planar graph with one designated face will be called a brick and this designated face will be called the perimeter of the brick. Without loss of generality we assume that the perimeter is the outer (infinite) face of the plane drawing of the brick. The first step of our reduction is to find 2-approxiate Steiner tree in . Next, we cut the plane open along tree (see Figure 1) to obtain the graph . Now all terminals lie on one face in whereas the optimal Steiner tree in is cut into smaller trees in each spanning some subset of terminals. As we do not know how exactly the optimal tree will be cut, we will prove that a single polynomial kernel exists for all possible subsets of terminals on the perimeter, i.e., the kernel will contain some optimal Steiner tree for every  possible subset of terminals on the perimeter. This is stated in the following theorem.

Theorem 2. Let be a brick. Then one can find in polynomial time a subgraph of such that

  • ,
  • is polynomial in ,
  • for every set , contains some optimal Steiner tree in that connects .

The idea behind the proof of Theorem 2 is to apply it recursively on subbricks (subgraphs enclosed by a simple cycle) of the given brick . The main challenge is to devise an appropriate way to decompose into subbricks, so that their ``measure' decreases. Here we use the perimeter of a brick as a potential that measures the progress of the algorithm.

partitionFigure 2. An optimal Steiner tree and how it partitions the brick into smaller bricks .

Intuitively, we would want to do the following. Let be a tree in that connects a subset of the vertices on the perimeter of . Then splits into a number of smaller bricks , formed by the finite faces of (see Figure 2). We recurse on bricks , obtaining graphs , and return . We can prove that this decomposition yields a polynomial bound on if (i) all bricks have multiplicatively smaller perimeter than , and (ii) the sum of the perimeters of the subbricks is linear in the perimeter of .

In this approach, there are two clear issues that need to be solved. The first issue is that we need an algorithm to decide whether there is a tree for which the induced set of subbricks satisfies conditions (i) and (ii). We design a dynamic programming algorithm that either correctly decides that no such tree exists, or finds a set of subbricks of that satisfies condition (i) and (ii). In the latter case, we can recurse on each of those subbricks.

doubleFigure 3. An optimal Steiner tree that connects a set of vertices on the perimeter of and that consists of two small trees that are connected by a long path ; note that both bricks neighbouring may have perimeter very close to .

The second issue is that there might be no trees for which the induced set of subbricks satisfies conditions (i) and (ii). In this case, optimal Steiner trees, which are a natural candidate for such partitioning trees , behave in a specific way. For example, consider the tree of Figure 3, which consists of two small trees , that lie on opposite sides of the brick and that are connected through a shortest path (of length slightly less than ). Then both faces of that neighbour may have perimeter almost equal to , thus blocking our default decomposition approach.

pineapple2
Figure 4. A cycle that (in particular) hides the small trees in the ring between and , and a subsequent decomposition of into smaller bricks.

To address this second issue, we propose a completely different decomposition - the pineapple decomposition. Intuitively, we find a cycle of length linear in that lies close to , such that all vertices of degree three or more of any optimal Steiner tree are hidden in the ring between and (see Figure 4). We then decompose the ring between and into a number of smaller bricks. We recursively apply Theorem 2 to these bricks, and return the result of these recursive calls together with a set of shortest paths inside between any pair of vertices on . The main technical difficulty is to prove that such circle exists. If you would like to learn more on how it works, you can still attend our talk during the coming FOCS in Philadelphia on Sunday at 11:05, or have look into the full version of the paper on arXiv. Additionally to the above result, the paper contains similar results for planar Steiner forest problem, planar edge multiway cut, as well as some generalization of these results to weighted graphs.