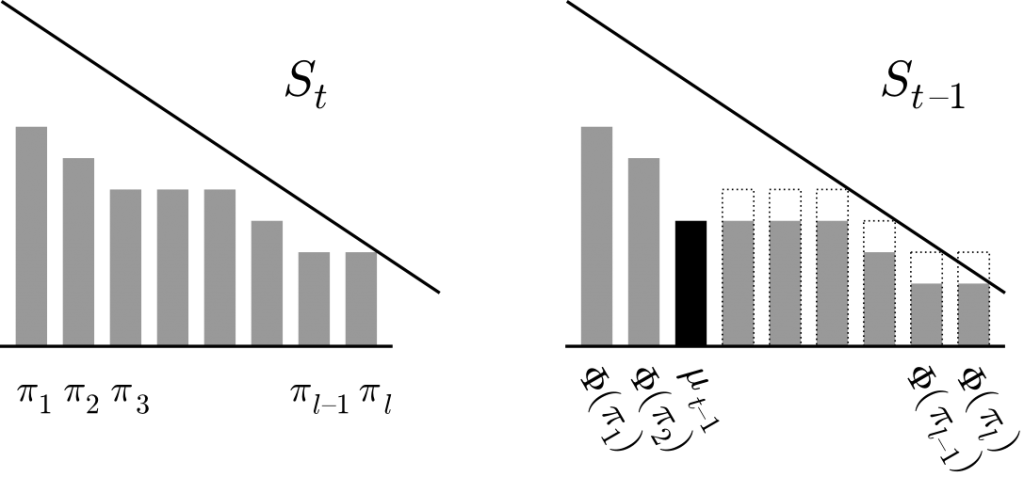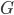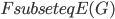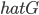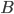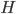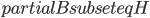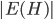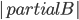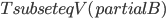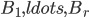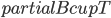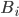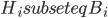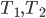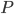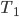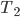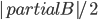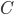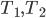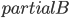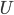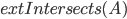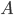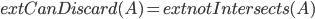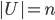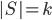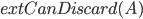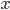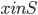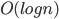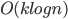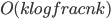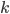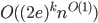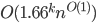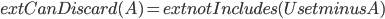Monthly Archives: October 2014

Online bipartite matching in offline time

Posted on by
Reply

In 1973 Hopcroft and Karp gave a very nice 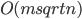time algorithm computing a maximum matching in unweighted bipartite graphs. This algorithm turned out to be the milestone that is hard to beat. The bipartite maximum matching problem has been studied in many different flavors such as online, approximate, dynamic, randomized or the combination of the above. The HK algorithm was improved for sufficiently dense and sufficiently sparse graphs. Nevertheless, for the general case, despite of the wide interest, little improvement over HK was obtained. This is somewhat intriguing, as no reasonable example certifies that the bound for the running time of HK is in fact tight. The HK algorithm is of offline nature and relies heavily on receiving the whole graph before processing it. On the quest for making some progress on the subject matter we aimed for the dynamic setting. Say the vertices need to be matched as they show up in the graph, so some re-matching is allowed and the maximum matching needs to be maintained at all times. Can one do better than simply finding any augmenting path each time a new vertex appears?

Let us narrow down the dynamic scenario we consider: say only the vertices of one side of the graph come in online, and at the time they show up they reveal all their adjacent edges. This scenario is easily motivated as follows.
There is a set of servers and a set of jobs to be executed on these servers. Every job comes with a list of servers capable of performing the job. Of course it is reasonable to serve as many jobs as possible, hence the maximum job-server matching is highly desired. Having that motivation in mind, an online scenario seems to be the most natural: jobs come in online one at the time, and request to be matched to one of the chosen servers. We care to match the job whenever its possible, so we allow some busy servers to be reallocated.
Now the question is, what is a good way of reallocating the servers, so that the dynamic algorithm can benefit from it? We adopt the following measure: each reallocation involves some reallocating cost. We want to minimize the cost of reallocating the servers.

We associate with each server 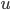an attribute called 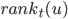, which states how many times the server has been reallocated in the entire process. The parameter 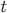stands for time. We see the entire process of adding jobs as a sequence of turns, in each turn a new job appears with the list of eligible servers. The attribute 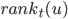describes the number of times 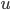was reallocated up to turn 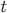. These attributes guide us when we search for augmenting paths. We try to avoid servers with high ranks. This should distribute the necessary reallocations more or less evenly among the servers.

In order to follow this approach, a certain greedy strategy comes to mind. When trying to match a new job, choose the augmenting path which minimizes the maximum rank of a server along this path. This strategy has one substantial disadvantage. If any augmenting path that we can choose to match the new job contains a vertex of high rank 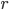, then we are allowed to rematch all servers of ranks at most 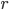. That is clearly an overhead. We hence define another attribute, 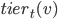, for every job 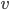. This attribute says what is the rank of the lowest ranked path from 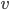to any unmatched server. When we try to match job 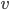, we search for the alternating path along which the tiers of jobs do not increase. We call such a path a tiered path. In other words, a tiered path minimizes the maximal rank on its every suffix. This seems natural: why to re-enter vertices of high rank when we can avoid them.

It turns out that this simple strategy does quite well: the ranks (and hence also the tiers) do not grow above 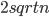. That means, that each server gets reallocated at most 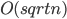times. This is already interesting. Moreover, if we knew how to efficiently choose the right augmenting paths, the total work would be 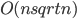. We have an algorithm that finds all the augmenting paths in the total time 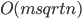, what matches the offline time of HK.

So let us first take a look on how the bound on the maximum rank is obtained. First of all, we direct the edges of the graph according to the current matching: the matched edges point from servers to jobs, while the unmatched edges point the other way around. Now, directed paths are alternating, so in each turn we need to find a directed path from the new job to a free server and reverse the edges along the path. We first show that the servers of high ranks are far from the unoccupied servers: the directed distance from any server 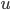to an unmatched server in turn 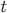is at least .

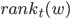We now look at any set 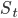of vertex disjoint directed paths covering all free servers in turn 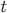before applying the augmenting path. Note, that there are no outgoing edges from free servers, so the paths end there. The rank of the directed path present in the graph in turn 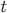is the maximum rank of a server on it. Let's call the augmenting path applied in turn . We analyze the augmentation process backwards. In turn , before applying , there exists a set of vertex disjoint paths 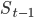covering free servers, such that:

  • every path 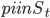has its counterpart 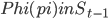, where 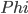is an injection
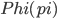  • has rank at least as high as , unless 's rank is smaller or equal to one plus the rank of : then the rank of 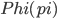may be one less then the rank of
  • there is a path in 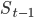that is not in the image of 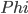and has rank at least the rank of

This observation may be translated as follows. Let us, for every path in 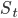, draw a vertical bar of height equal to its rank. Let us now sort the bars in descending order and put them next to each other, as shown in Figure 1 to the left. These bars are the ranks of the paths in turn 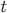. When we take a step back to turn , we have another set of bars corresponding to paths from turn , where one additional bar pops out. Moreover, some bars may have decreased by one, but all the bars that decreased are dominated (with respect to height) by the newly added bar. This is shown in Figure 1 to the right. The process ends when we reach turn , and there is bars of height zero.

ledge_01

Now we move to bounding the maximum rank. The maximum rank, say 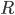, will appear on some path in some turn 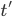. We take a look at set 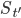consisting of this single path. There is only one bar of height 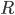. In the previous turn, either there is still a bar of the height 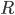, or there are two bars of height 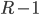. Every time the bars decrease, there comes another bar that dominates the decreased bars. Somewhere on the way back to turn 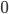there is a set of bars with the sum of heights quadratic in 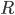. The bars, however, correspond to vertex disjoint paths, and the heights of the bars are the lower bounds on the lengths of these paths. Hence, there is 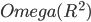vertices in the graph and .

bars_02

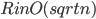The question that remains is whether we are able to efficiently find these paths. The main problem here is that we need augmenting paths where the tiers of jobs along the path do not increase. This is not a good news: the tiers are difficult to maintain upon the reversal of the edges on the entire augmenting path. The idea is to maintain them in a lazy manner. For each job 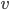, instead of its actual tier, the algorithm maintains an attribute 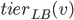. Subscript LB stands for lower bound, as we maintain the invariant that 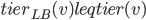. When a new vertex 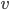turns up in some turn, 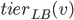is set to 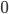. The algorithm repeatedly tries to find (in the directed graph) a tiered (according to the maintained lower bounds for tiers) directed path from 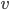to a free server. It executes a search routine from 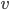, traversing only the vertices with ranks and 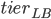's bounded by 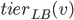. Once a job 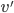with 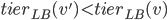is discovered, the upper bound on the ranks and 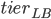's of vertices visited next is recursively set to 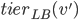. This goes on until one of the two things happen. It might be that a free server is discovered. Then we found an augmenting path, along which the 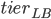's of the vertices are their actual tiers (the path that we found is a witness for that). We reverse the edges along the augmenting path and increase the ranks of the reallocated servers. It might also happen that the search fails. This means, that the algorithm detects a group of vertices whose 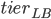's are lower than their actual tiers. The algorithm then rightfully increases the 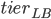's associated with these vertices. It continues the search from the point where it failed. The difference is that now it can search further, as it is allowed to visit vertices with higher 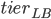's than before. The general idea is that whenever a vertex is visited by the algorithm, either its 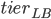or its rank is increased. Unfortunately upon every such visit the algorithm may touch all the edges adjacent to the visited vertex. These edges, however, will be touched in total 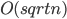times each. The total time amounts to .

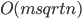How pineapples help finding Steiner trees?

Posted on by
Reply

The Bratislava Declaration of Young Researchers is something I was involved in recently. Its preparation was inspired by Slovak Presidency of the EU and it was presented on today's informal Council of Ministers responsible for competitiveness (Research). I hope this will have some follow up, as current trend in funding research in EU is in my opinion (and not only my as this declaration shows) going in the wrong direction.
Recently with Marcin Pilipczuk, Micha? Pilipczuk and Erik Jan van Leeuwen we were able to prove that the Steiner Tree problem has a polynomial kernel on unweighted planar graphs. So far this was one of few problems where such kernel seemed possible, but existing tools (e.g. theory of bidimensionality) were unable to deliver it. Essentially, we were able to prove the following theorem.

Theorem 1. Let be a planar Steiner tree instance, and let be the cost of optimum tree connecting terminals in the unweighted graph . One can in polynomial time find a set of edges of size polynomial in that contains an optimal Steiner tree connecting in .

cutopen Figure 1. The process of cutting open the graph along the tree .

Let us shortly discuss the idea of the proof of this theorem. The most non-trivial part of it is the pineapple decomposition. In order to give you a glimpse on this decomposition we will first reduce the problem to the simpler case where all terminals lie on one designated face. Such planar graph with one designated face will be called a brick and this designated face will be called the perimeter of the brick. Without loss of generality we assume that the perimeter is the outer (infinite) face of the plane drawing of the brick. The first step of our reduction is to find 2-approxiate Steiner tree in . Next, we cut the plane open along tree (see Figure 1) to obtain the graph . Now all terminals lie on one face in whereas the optimal Steiner tree in is cut into smaller trees in each spanning some subset of terminals. As we do not know how exactly the optimal tree will be cut, we will prove that a single polynomial kernel exists for all possible subsets of terminals on the perimeter, i.e., the kernel will contain some optimal Steiner tree for every  possible subset of terminals on the perimeter. This is stated in the following theorem.

Theorem 2. Let be a brick. Then one can find in polynomial time a subgraph of such that

  • ,
  • is polynomial in ,
  • for every set , contains some optimal Steiner tree in that connects .

The idea behind the proof of Theorem 2 is to apply it recursively on subbricks (subgraphs enclosed by a simple cycle) of the given brick . The main challenge is to devise an appropriate way to decompose into subbricks, so that their ``measure' decreases. Here we use the perimeter of a brick as a potential that measures the progress of the algorithm.

partitionFigure 2. An optimal Steiner tree and how it partitions the brick into smaller bricks .

Intuitively, we would want to do the following. Let be a tree in that connects a subset of the vertices on the perimeter of . Then splits into a number of smaller bricks , formed by the finite faces of (see Figure 2). We recurse on bricks , obtaining graphs , and return . We can prove that this decomposition yields a polynomial bound on if (i) all bricks have multiplicatively smaller perimeter than , and (ii) the sum of the perimeters of the subbricks is linear in the perimeter of .

In this approach, there are two clear issues that need to be solved. The first issue is that we need an algorithm to decide whether there is a tree for which the induced set of subbricks satisfies conditions (i) and (ii). We design a dynamic programming algorithm that either correctly decides that no such tree exists, or finds a set of subbricks of that satisfies condition (i) and (ii). In the latter case, we can recurse on each of those subbricks.

doubleFigure 3. An optimal Steiner tree that connects a set of vertices on the perimeter of and that consists of two small trees that are connected by a long path ; note that both bricks neighbouring may have perimeter very close to .

The second issue is that there might be no trees for which the induced set of subbricks satisfies conditions (i) and (ii). In this case, optimal Steiner trees, which are a natural candidate for such partitioning trees , behave in a specific way. For example, consider the tree of Figure 3, which consists of two small trees , that lie on opposite sides of the brick and that are connected through a shortest path (of length slightly less than ). Then both faces of that neighbour may have perimeter almost equal to , thus blocking our default decomposition approach.

pineapple2
Figure 4. A cycle that (in particular) hides the small trees in the ring between and , and a subsequent decomposition of into smaller bricks.

To address this second issue, we propose a completely different decomposition - the pineapple decomposition. Intuitively, we find a cycle of length linear in that lies close to , such that all vertices of degree three or more of any optimal Steiner tree are hidden in the ring between and (see Figure 4). We then decompose the ring between and into a number of smaller bricks. We recursively apply Theorem 2 to these bricks, and return the result of these recursive calls together with a set of shortest paths inside between any pair of vertices on . The main technical difficulty is to prove that such circle exists. If you would like to learn more on how it works, you can still attend our talk during the coming FOCS in Philadelphia on Sunday at 11:05, or have look into the full version of the paper on arXiv. Additionally to the above result, the paper contains similar results for planar Steiner forest problem, planar edge multiway cut, as well as some generalization of these results to weighted graphs.

FPT algorithms and syphilis

Posted on by
Reply

Long long time ago, ed actually in 1943, US Army was recruiting a lot of soldiers. Each of the recruits had to be subject of some medical examination, and in particular they were tested against syphilis. However, performing a single test was quite expensive. Then they came up with the following idea. Pick blood samples from a group of soldiers, mix them into a one big sample and perform the test on it. If the test is positive, there is at least one infected soldier in the group. But if it is negative, we know that all of the soldiers in the group are healthy and we just saved a lot of tests. It becomes then an interesting problem to devise a method which uses this observation to find the exact group of infected recruits among all the candidates with some nice bound on the number of tests. Without any additional assumptions there is not much you can do (exercise: do you see why?) but in this case we expect that the number of infected candidates is quite small. Then in fact you can save a lot and this story gave rise to the whole area called group testing.

Group testing is a rich field and includes a variety of models. Let us focus on the following one. We are given a universe and we want to find a hidden subset  of . We can aquire information only by asking queries to the intersection oracle, i.e., for a given subset , answers true if and only if has a nonempty intersection with . Moreover, we can decide which set we query based on previous answers. The goal is to use few queries. There are many algorithms for this problem, but I'm going to describe you my favourite one, called the bisecting algorithm. It dates back to early seventies and is due to Hwang, one of the fathers of combinatorial group testing. As you may expect from the name, it is a generalization of binary search. A simple observation is that once answers false, we can safely discard and otherwise we know that contains at least one element of . So assume that in the algorithm we use a  oracle, implemented just as . The algorithm works as in the animation below (choose FitPage in the zoom box and keep clicking the arrow down) :

View Fullscreen

So, basically, we have a partition of a universe (initially equal ) with the property that every set in the partition contains at least one element of . We examine sets of the partition one by one. Each set is divided into two halves and we query whether we can discard one of them. At some point we query a singleton and then we either discard it or find an element of . I hope it is clear now, but let me paste a pseudocode as well. bisection How many queries do we perform? Let and . Call a query positive if the answer is Yes, negative otherwise. For a negative query  we know that there is . Assign this query to . Note that for every there are  queried sets assigned to it, because if we consider the queries in the order of asking them, every set is roughly  twice smaller than the previous one. So there are  negative queries. Every set from a positive query is a half of a set from a (different!) negative query, so the total number of positive queries is bounded by the total number of negative ones. Hence we have   queries in total. A slightly more careful analysis (see Lemma 2.1 here) gives . Cool, isn't it? Especially given that we hopefully do not expect a large fraction of infected soldiers...

Great, but is there a connection of all of that with the FPT algorithms from the title? Yes, there is one. Consider for example the k-PATH problem: given a graph and a number we want to find a path of length . The corresponding decision problem is NP-complete, as a generalization of Hamiltonian Path. However, it turns out that when  is small, you can solve it pretty fast. Perhaps you know the famous Color Coding algorithm by Alon, Yuster and Zwick which solves it in . However, one can do better: Björklund, Husfeldt, Kaski and Koivisto presented a  -time Monte-Carlo algorithm! The only catch is that it only solves the decision problem. Indeed, it uses the Schwartz-Zippel lemma and when it answers YES, there is no way to trace back the path from the computation.

Now, let the universe   be the edge set of our graph. We want to find one of (possibly many) -subsets of corresponding to -edge paths in our graph and the Björklund et al's algorithm is an inclusion oracle, which tells you whether a given set of edges contains one of these subsets. So this is not exactly the same problem as before, but sounds pretty similar... Indeed, again we can implement the   oracle, i.e., . So it seems we can use the bisecting algorithm to find a -path with only  queries to the decision algorithm! Correct?

Well, not exactly. The problem is the oracle is a Monte Carlo algorithm, more precisely it reports false negatives with probability at most, say, 1/4. Together with Andreas Björklund and Petteri Kaski we showed that a surprisingly simple patch to the bisecting algortihm works pretty nice in the randomized setting. The patch is as follows. Once the bisecting algorithm finishes in the randomized setting, we have a superset of a solution. Then, as long as we have more than  candidate elements, we pick one by one, in a FIFO manner, and check whether we can discard this single element. We show that the expected number of queries is . (Actually, we conjecture it is optimal, i.e., you have to loose a bit compared to the slightly better   in the deterministic setting.) As a consequence, we get a pretty fast implementation of finding  -paths. For example, a (unique) 14-vertex path is found in a 1000-vertex graph well below one minute on a standard PC. Not bad for an NP-complete problem, I would say. Let me add that the Schwartz-Zippel approach is used in a number of FPT algorithms and in many cases the corresponding search problem can be cast in the inclusion oracle model mentioned above. Examples include k-packing, Steiner cycle, rural postman, graph motif and more.

If you want to learn more, see the paper or slides from my recent ESA talk!