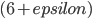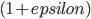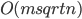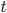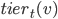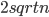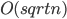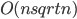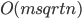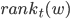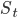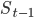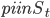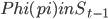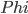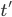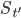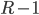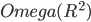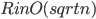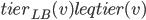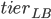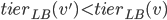Guest post by Aleksander Mądry
This summer, on June 6-8 in Paris, we will be having a new algorithmic event: Highlights of Algorithms 2016 (HALG 2016) conference.
This conference will be quite unlike the conferences we are all used to. First of all, it will consist mainly of invited talks and tutorials, accompanied by a smaller number of contributed talks and posters. Secondly, there will be no conference proceedings, i.e., presenting work already published at a different venue or journal (or to be submitted there) is absolutely welcome and even encouraged.
The call for submissions of contributed short talks and posters has been just posted online. The program committee is currently in the process of selecting invited speakers (partially based on the nominations from the community).
We already have a number of very exciting speakers committed and we expect to add a few more names shortly.
The intention here is to make HALG a forum for presenting the highlights of some of the most exciting recent developments in algorithms, discussing potential further advances in this area, as well as networking and initiating new collaborations. In a way, we want HALG to be a place one can go to catch up on what are the hottest results/topics
at the moment, as well as what one missed by not being able to attend all the STOC/FOCS/SODA/ESA/ICALP/PODC/ITCS/… conferences that year.
We believe that this kind of venue is very much needed today and will help to make our community stronger and more cohesive. In particular, we hope that the success of the first edition will make HALG become a recurring event. In fact, HALG draws some inspiration from Highlights of Logic, Games and Automata (HLGA) conference series that became very successful in its respective community already. There are some differences in how both conferences are constructed: HALG will concentrate on invited talks with some contributed talks, whereas HLGA was only having short contributed talks so far; but the overall premise is the same and seems to be working very well. (We also heard some rumors that the next edition of HLGA will move in the direction of HALG and have invited talks too.)
In any case, the HALG 2016 in Paris should be a lot of fun. We hope to see many of you there! So please submit your work to HALG.
This year for the first time we will have a new algorithmic event taking place - Highlights of Algorithms 2016 (HALG 2016) will be in Paris, June 6-8, 2016. I actually hope that this will become a recurring event in European CS calendar. Some crazy idea for future could be to collocate it with Highlights of Logic, Games and Automata conference that inspired a lot creation of HALG. There are, however, differences in how both conferences are organized. HALG will concentrate on invited talks with some contributed talks, whereas the logic Highlights was only having short contributed talks. I heard some rumors that the next edition of Highlights of Logic, Games and Automata will move into the direction of HALG and have invited talks. Anyway, I hope you will plan to attend the event as it already seem that we will have and interesting program with many highlights of recent developments in algorithms.
The HALG conference has opened the registration and the program is available as well - see the links below. The program looks very interesting so I hope many of you will be coming.
Highlights of Algorithms - HALG 2016
June 6-8, 2016, Paris, France
http://highlightsofalgorithms.org/
The Highlights of Algorithms conference is designed to be a forum for presenting the highlights of recent developments in algorithms and for discussing potential further advances in this area. The conference will provide a broad picture of the latest research in algorithms through a series of survey and invited talks, as well as possibility for all researchers and students to present their recent results through a series of short talks and poster presentations. Attending the Highlights of Algorithms conference will also be an opportunity for networking and meeting leading researchers in algorithms.
The registration for the Highlights of Algorithms conference is open.
To register, please visit the link at http://highlightsofalgorithms.org/registration/. (early registration is due April 30)
A preliminary program is available online at http://highlightsofalgorithms.org/program/.
The program is packed with 28 invited talks and with even a larger number of short contributions.
Those interested in attending the conference are advised to book accommodation as early as possible (given the high hotel prices in Paris).
Guest post by Aleksander Mądry
This summer, on June 6-8 in Paris, we will be having a new algorithmic event: Highlights of Algorithms 2016 (HALG 2016) conference.
This conference will be quite unlike the conferences we are all used to. First of all, it will consist mainly of invited talks and tutorials, accompanied by a smaller number of contributed talks and posters. Secondly, there will be no conference proceedings, i.e., presenting work already published at a different venue or journal (or to be submitted there) is absolutely welcome and even encouraged.
The call for submissions of contributed short talks and posters has been just posted online. The program committee is currently in the process of selecting invited speakers (partially based on the nominations from the community).
We already have a number of very exciting speakers committed and we expect to add a few more names shortly.
The intention here is to make HALG a forum for presenting the highlights of some of the most exciting recent developments in algorithms, discussing potential further advances in this area, as well as networking and initiating new collaborations. In a way, we want HALG to be a place one can go to catch up on what are the hottest results/topics
at the moment, as well as what one missed by not being able to attend all the STOC/FOCS/SODA/ESA/ICALP/PODC/ITCS/… conferences that year.
We believe that this kind of venue is very much needed today and will help to make our community stronger and more cohesive. In particular, we hope that the success of the first edition will make HALG become a recurring event. In fact, HALG draws some inspiration from Highlights of Logic, Games and Automata (HLGA) conference series that became very successful in its respective community already. There are some differences in how both conferences are constructed: HALG will concentrate on invited talks with some contributed talks, whereas HLGA was only having short contributed talks so far; but the overall premise is the same and seems to be working very well. (We also heard some rumors that the next edition of HLGA will move in the direction of HALG and have invited talks too.)
In any case, the HALG 2016 in Paris should be a lot of fun. We hope to see many of you there! So please submit your work to HALG.
The ESA call for papers is out: http://conferences.au.dk/algo16/esa/. The submission deadline is April 21, 23:59 AoE, 2016, whereas the notifications will be send out no later than on June 9, 2016. I hope there will be many submissions to keep us in the PC busy during this time. Anyway, if you plan to submit something, you might read (or maybe read again) the post by Boaz Barak: http://windowsontheory.org/2014/02/09/advice-for-focs-authors/. It contains advice on how to increase your chances that your paper gets accepted to a conference - FOCS in this case. The same applies to most conferences and "putting the worst foot forward" is often the hardest part. However, believe me that doing the opposite usually hurts even more.