According to the report by Foundation for Polish Science working in Poland can be seen as hurting your scientific carrier.
We do not really agree with it and the above meme was meant to be self-ironic. It of course could be better - as everywhere. Anyway, if you would like to see how it is to work in Poland we have two postdoc positions in algorithms open - see the call.
We have given to the students a task to promote algorithms on the web. This is what came up:
Click here for a version in polish.
During my recent visit to Warwick University I had the pleasure of working with Maxim Sviridenko. I had known many of his papers, since we both work on problems related to TSP. However, I have not met him before. One thing I learned from my visit is that Maxim is a really nice guy, another is that he is really fond of scheduling problems. It is no surprise then, that we started working on a problem that sits right in the intersection of scheduling and TSP related problems, i.e. no-wait flow shop scheduling (NWFS). There were not too many results known for this problem, in particular no hardness of approximation results. However, a PTAS was known for a constant number of machines, and the general version was known to be a special case of ATSP. Since we only know an O(log n/ log log n)-approximation algorithm for the latter, NWFS seemed to be a very attractive target, a possible first step towards obtaining better results for ATSP. In particular, it is for this reason that NWFS was mentioned in the open problem list of Shmoys and Williamson in their book on approximation algorithms.
As you no doubt have already guessed, either from the title of this post, or from the past tense in one of the previous sentences, it did not exactly work as planned. However, we got some really nice results on the way. It turned out, that not only is NWFS APX-hard, but it is also ATSP-hard. The latter means that c-approximation for NWFS (where c is possibly a function of the number of jobs n) implies c(1+?)-approximation for ATSP for any ?>0. Given the existence of a PTAS for a constant number of machines, this is a rather surprising result. I will try to present the core idea here, which I believe is quite elegant, without engaging in too many technical details.
No-wait flow shop
In the no-wait flow shop problem, you are give a set of n jobs J_1,...,J_n on m machines M_1,...,M_m. Each job is a sequence of m operations, one for each machine, with processing time t_ij for i-th job on j-th machine. As usual, you are supposed schedule all the jobs and minimize the total makespan of the schedule. The unique features of this problem are the following:
Because of the no-wait constraint, this problem can behave in a very unexpected manner. For example, speeding up one of the machines can result in increasing the optimum makespan! (see Spieksma, Woeginger The no-wait flow-shop paradox)
From NWFS to ATSP
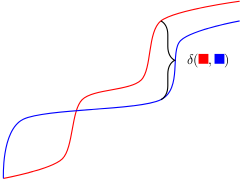
There are many distance functions that can be defined on no-wait flow shop jobs. One possibility is to define ?(i,j) as the minimum time we need to wait to start J_j after starting J_i. This is illustrated in the figure below.
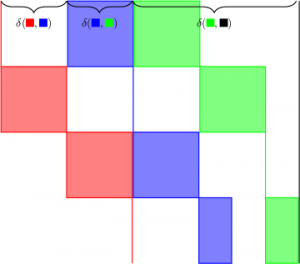
The set of all jobs with the distance function ? defines a semi-metric (almost, ?(i,i) <> 0 but that is easy to fix). Schedules correspond to paths in this semi-metric. The makespan of a schedule is equal to the length of the corresponding path + the total length of the last job. To handle the last job we do what the picture suggest, i.e. add a dummy job consisting of all zeros and then reduce to ATSP (and not ATSP path!).
From ATSP to NWFS
To see how one can go in the opposite direction, imagine a flow shop instance with a very large number of machines and very small processing times for each operation. Then the picture looks more like this.
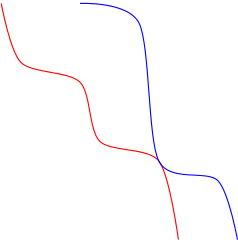
There is now a second way to (approximately) measure ?(i,j). Simply align the starting points of both jobs and look for a point where J_j is the most to the left of J_i.
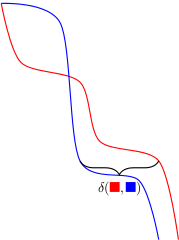
If we now rotate the picture, we can see that the jobs really are just monotone functions and for two such functions f, g, we have ?(f,g) = max(f-g).
Now, here is the key fact - the function space discribed above is a universal space for all semi-metrics. More precisely: Any n-point semi-metric embeds isometrically in R^n with distance defined as ?(x,y) = max(x,y). This result is a "directed" version of the universality of l_? for metrics and the proof is almost identical.
To get actual hardness results one needs to control the number of machines and embedding errors. Also, one needs to somehow handle the last term in the flow shop objective function that is not related to ?, i.e. the length of the last job. But what the above considerations already show that no-wait flow shop distance functions are really no easier than general semi-metrics, which is the heart of the argument.
Over? Not quite...
Is this the end of story? Most likely yes, if one is only interested in using NWFS to attack ATSP. However, the approximability of NWFS itself is still wide open. On one had, we have a PTAS, on the other we give a O(log m)-approximation algorithm in our paper (a variation on Frieze, Galbiati, Maffioli). What happens for moderate values of m, say m=log n, remains a mistery.
I decided to give a one-semester course entitled "On a Cycle in a Graph" next year. At first sight it might seem that this topic is trivial, but the algorithmic aspects of finding cycles with given properties can easily get complicated. Maybe it is better to say that they almost immediately become interesting. For example, what are the fastest algorithms for finding shortest cycles in graphs? This question was the topic of two FOCS papers recently - in 2011 and 2012. These papers have shown that in directed and undirected graphs a shortest cycle can be found in O(Wn^omega) time, when the edges of the graph are integral in the range [-W,W]. On the other hand, for planar graphs we have shown last year (ESA 2011) that this problem can be solved in O(n log log n) time. The paper studies undirected graphs, but the same technique can be applied to the directed case as well. The conjecture is that this should be possible in linear time! Similarly, it should be possible to find in linear time a shortest cycle that would contain s inside and t outside, for given s and t. This is exactly the min st-cut problem in planar graphs. Here, the fastest algorithm works in O(n log log n) time (STOC 2011). This, for me, is currently the most intriguing open problem in planar graphs. There are much more aspects of shortest cycles, e.g., finding shortest even length cycle seems much easier then finding shortest odd length cycle (ICALP '96).
By just adding another condition "passing through every vertex" to "shortest" one gets the TSP problem - this is what tigers like most. This problem in graphical case has witnessed some interesting progress in the last year (starting from FOCS 2011). Nevertheless, for the (general) metric case the Christofides algorithm remains the best. Finding longest cycles starts yet another related story, and leads us to techniques like color-coding (STOC '94).
General cycles are complicated, but even length 3 cycles -- triangles -- are not so easy. Finding minimum weight triangle (when edges are negative), seems to be as hard as the general problem as long as we want to get subqubic algorithms (FOCS 2010). Similarly, counting triangles in graphs has become one of the challenges in streaming algorithms. The number of triangles seems to be the simplest criteria to tell a random network form a social network apart. The social networks tend to be huge, so "subcubic" can here only mean linear time.
One of my favorite topic is the connection between cycles and matchings, which manifests itself in several nice relations. A minimum weight cycle cover problem (2-factor problem) can be solved using minimum weight perfect matchings. Or the problem of computing shortest distances from given source, can be seen as the dual problem to the shortest cycle problem - as shown by Gabow (FOCS '83). Finally, one should mention the tramp-steamer problem, i.e., the minimum mean-weight cycle problem. It is somewhat astonishing that such globally minimum cycle can be efficiently found, whereas the application to finding min-cost max-flow is a nice story as well.
To summarize, there is a lot to tell and it looks rather easy to fill a course with topics related to cycles in graphs. There are much more topics that can be added and probably you could name a few. However, more importantly huge fraction of these results happened just very recently. These topic are interesting for the algorithmic community (it is easy to get into good conferences) and there are a lot of nice open problems.
Recently our algorithms group has been extended by four (!) new faculty members:
Welcome on board!
This is perhaps a good opportunity to mention that our faculty have just announced a call for applications for attractive post-doc positions. Perhaps our group will grow even more soon?
The FOCS presentation for our talk on Algorithmic Applications of Baur-Strassen’s Theorem... The interesting part is the 3D interpretation of the dual LP.
Back in 2006, I was a post-doc at MPI Saarbruecken in Kurt Mehlhorn's group. At that time, I started working on several TSP variants beginning with my collaboration with Kasia Paluch and Olek Mądry on the symmetric MAX-TSP. The most fascinating of these was not really a TSP variant, but a problem that is solved by a reduction to one - the Shortest Superstring Problem (SSP) in which you look for a shortest string containing a given set of strings as substrings. My fascination was even greater because of the fact that I felt absolutely certain that I had an idea to improve upon the already rather old result of Sweedyk (from 1991) giving 2 1/2-approximation, only somehow I could not quite make it work. The thing was that the same 2 1/2-approximation could be achieved by using a 2/3-approximation algorithm for MAX-ATSP from a paper by Heim Kaplan, Moshe Lewenstein, Nira Shafrir and Maxim Sviridenko, but just using that result as a black-box did not seem right. However, the proof of the 2/3-approximation there was rather complicated so I could not really put my finger on it.
Fast forward 7 years foward, after several unsuccessful attempts to improve upon the 2 1/2 factor, I stumbled upon a beatiful STACS paper again by Kasia Paluch, together with Khaled Elbassioni and Anke van Zuylen, which gives a new 2 1/2-approximation algorithm for MAX-ATSP. (If you have not yet read this paper, do it!) Obviously, I decided to try adapt this paper to my needs and use it to approximate SSP. That attempt failed completely after a rather heavy struggle. However, on the next day after realizing it was not going to work, it turned out the effort was not in vain - I had the right idea all along, only did not completely realize it. This was one of those crazy moments in research where you are obsessively trying to find something, only to find something completely different and unexpected, and equally or even more valuable!
I will not describe the approach here - that would necessarily be rather long, since the paper builds quite heavily on previous results. However, I am going to present this result at SODA 2013 in January. So if you want to learn more about how a 13 years old bound was improved, come to my talk in New Orleans, or even better chat with me over coffee. See you in 3 months!
Marcin
One of the talks that deeply fall into my memory was the talk on this paper at ICALP 2011, where the authors show that some important problem is NP-hard, settling a 15-year-old open problem. The talk was exactly as you expected it to be: there were gadgets, and more gadgets, and more and more gadgets, until they stopped to fit into the slide. The tradition of such a talk on ICALP was maintained in 2012 by Dániel Marx with his Planar Multiway Cut lower bound.
Recently I spotted a list every TCSer should do in its career. I think that a point "publish a paper that consists solely of one humongous hardness reduction" is definitely missing there.
I miss a few points from the aforementioned list, but at least this new one would be satisfied with our this years SODA paper on Edge Clique Cover. Yes, there is only one huge reduction in this paper. It proves that, essentially, to solve the Edge Clique Cover problem exactly, you cannot do anything better than apply easy reductions and go brute-force.
In Edge Clique Cover we ask to cover the edges of a given graph with a minimum number of cliques that are its subgraphs. This is equivalent to saying that we want to compute an intersection model of a given graph with minimum size of the universe. There are a few easy reduction rules, such as "do the obvious thing with isolated vertices and isolated edges" or "identify twins, i.e., vertices v, u with N[v] = N[u]" (see here for details). If we ask for k cliques (k-element universe), these reductions bring the size of the graph down to 2k. A brute-force algorithm runs in time exponential in the size of the graph, which gives double-exponential dependency on k.
We show a reduction that reduces (in polynomial time) an n-variable 3CNF-SAT formula to a Edge Clique Cover instance with k=O(log n). This shows that any significant improvement upon the brute-force algorithm on the reduced instance would yield a subexponential algorithm for 3CNF-SAT, which seems unlikely.
The key idea of our reduction is to use the cocktail party graph as the main gadget. While it has got a plenty of edge clique covers of size O(log n), the known reductions are not able to reduce it.
So, if you'll attend SODA'13 and you like to see some slides filled with gadgets, don't miss Michal's talk on our paper.
Last week we have hosted the 5th Workshop on Flexible Network Design. There have been a great number of interesting talks: http://fnd2012.mimuw.edu.pl/?q=node/4, and huge number of open problems. The open problems can be posted and discussed here: http://fnd2012.mimuw.edu.pl/qa.
Below there are some photos from the workshop.
